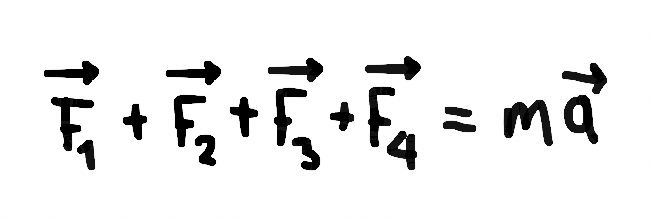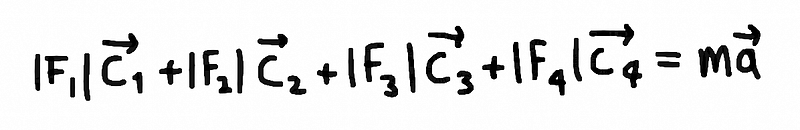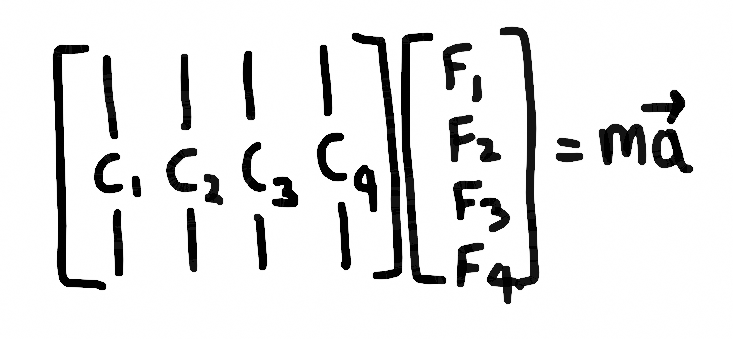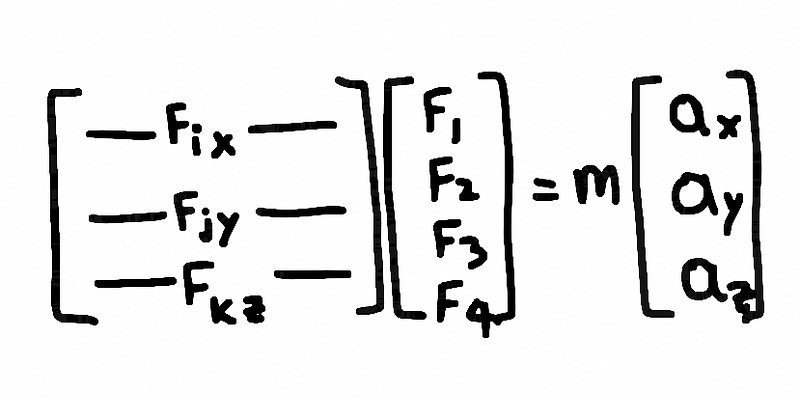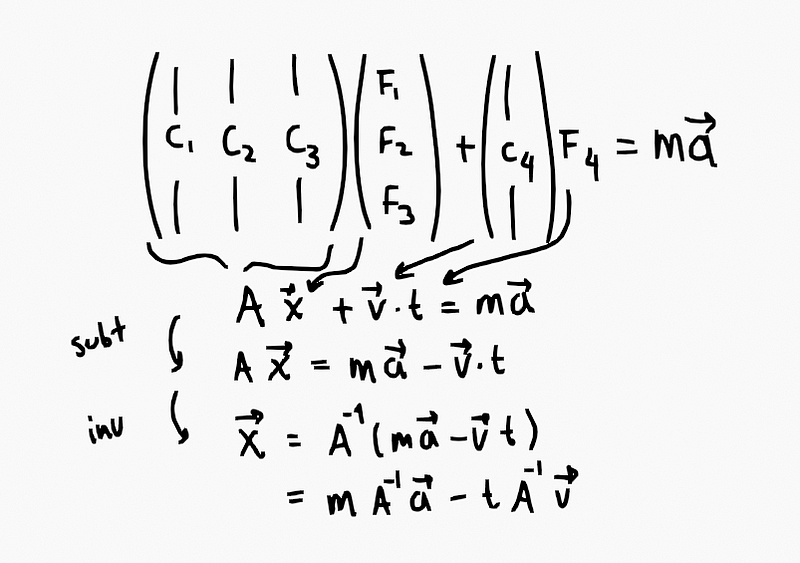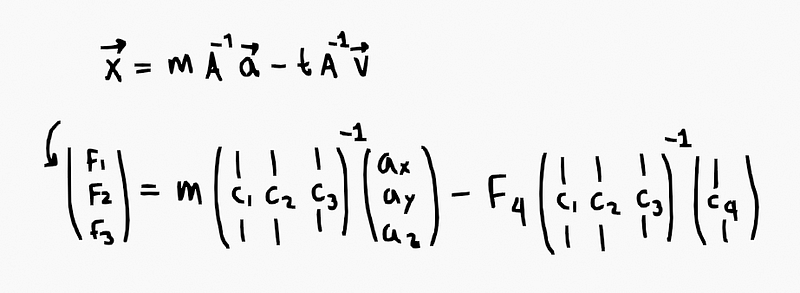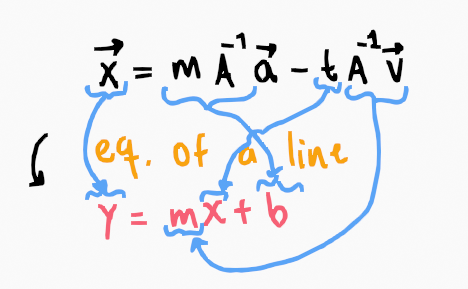Modeling a cable-suspended robot

Underdetermined system

Underdetermined systems are those that have more parameters than constraints.

Typically, each constraint reduces the number of free parameters, so if we pair a constraint with an individual parameter, we end up with an excess of parameters relative to the constraints.

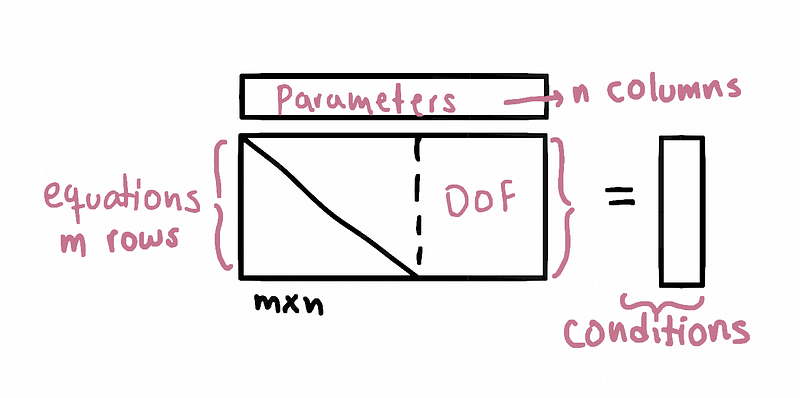
Illustration of DOF as the excess of parameters

We call this excess of parameters the degrees of freedom - DOF (in the context of linear algebra). These are the parameters that we can freely change and still obtain the same result. This parametric "movement," achieved by altering the parameter in a vector space without altering the outcome, occurs in the null space of the matrix.

Even though there are two cases in which a matrix is singular, we can easily identify an underdetermined system. This happens when expressing the matrix form and observing that it is wider, meaning it has more columns (parameters) than rows (constraints).

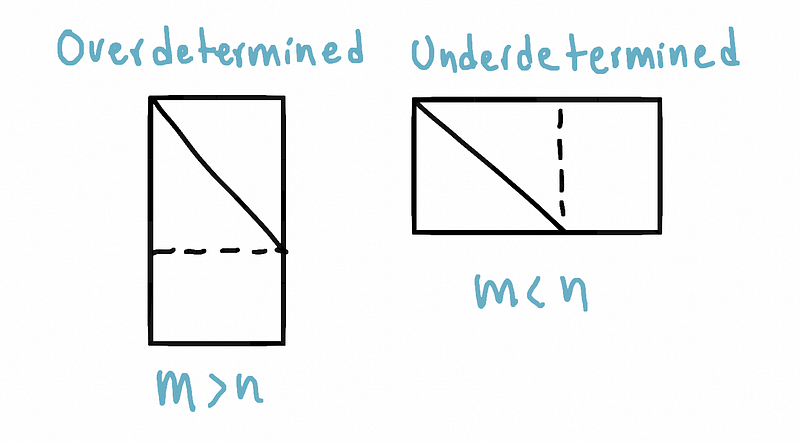
Shape of matrices; overdetermined vs underdetermined

Cable robot

A cable robot moves by manipulating cables, providing it with flexibility and precision in its movements. The application of forces through the cables enables it to perform various motions.

Cable robot prototype

It has many applications, with perhaps the most well-known being the transmission of aerial images in sports events.

Cable robot prototype in a stadium [hdri: Empty Football Stadium • HDRI Haven (hdri-haven.com)]

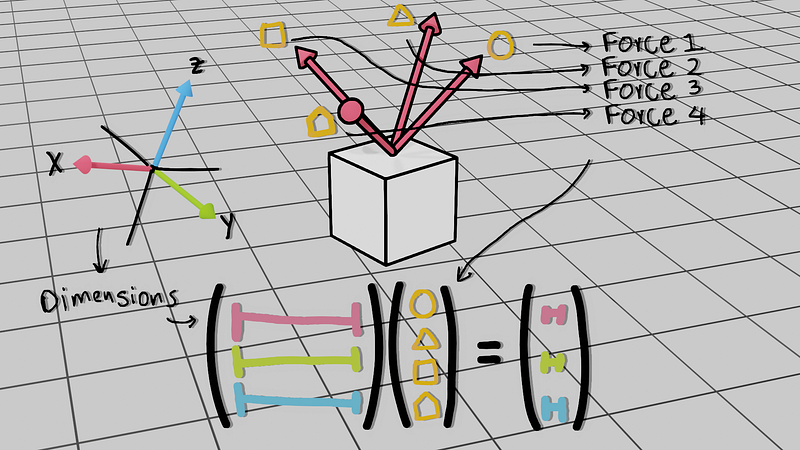
How can one model such a robot? To model a cable robot, we can consider each cable as a line segment, and thus, represent it as a vector in a three-dimensional space.

So, let's take, for example, 4 cables. We will then have 4 vectors pointing in 4 different directions (subsequently, 4 columns representing 4 parameters). And since it is a three-dimensional space, we will have 3 equations (subsequently, 3 rows).

But how do we represent them in matrix form?

Physical laws, formulating the model

What we want to model are the physical laws that allow the robot to move, enabling us to manipulate its movement as desired.

So, we formulate the laws of classical physics, particularly the second Newton's law: the sum of the forces equals the acceleration.

We have 4 forces as tridimensional vectors: (F1, F2, F3, F4), and we state that the sum is equal to mass times acceleration:

Second Newton's law

Writing each force individually: F1+F2+F3+F4=mass*acceleration

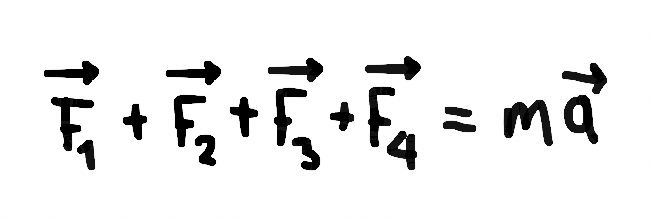
Second Newton's law, the addition of forces

We can take the direction of the cables as the direction of the tension force in the cables. So that each force is now a scalar quantity and not a tridimensional vector. This way we can express it as separated magnitude and direction:

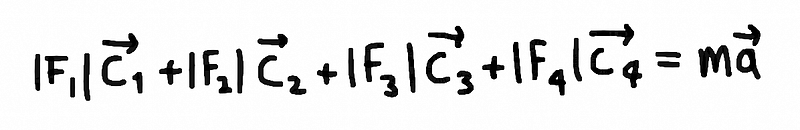
Second Newton's law, a separation between direction and magnitude

Now is easier to write its matrix form, each cable direction is also the respective force direction and represents a column, which is directly related to each force magnitude that represents a parameter.

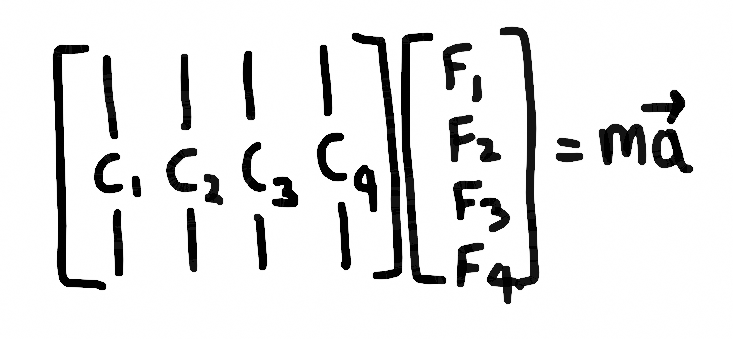
Second Newton's law, a matrix form with columns

On the row side, each row represents a dimension, as it is tridimensional we have three rows.

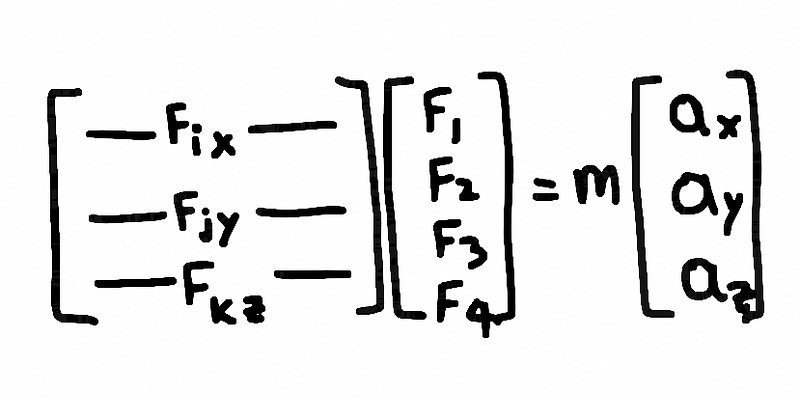
Second Newton's law, a matrix form with rows

Now, we attempt to solve the system… Oops! The determinant is zero. What do we do? because a matrix (m x n)= (3x4) gives us a singular matrix, we can't use the inverse of a matrix to solve the equation and find the distribution of force that leads to a desired acceleration.

Solution: Pseudo-inverse

Thanks to the proposal by Roger Penrose (now Nobel laureate) and others [Moore–Penrose inverse - Wikipedia], we have the pseudo-inverse. When applied, voilà! We obtain a combination of forces that constitutes a solution, actually the best one (the one which minimizes square sum).

But, is that all? Weren't there supposed to be infinite answers, and we found only one? What was it? The pseudo-inverse finds the one that minimizes the sum of the squared forces, analogous to the mean squared error, but what about the others?

Why does it minimize the sum of square forces? comment if want to know an explanation, it deserves its own story.

There are two sides to the pseudoinverse, one for underdetermined systems and the other for overdetermined systems. Here we are interested in the right pseudo-inverse.

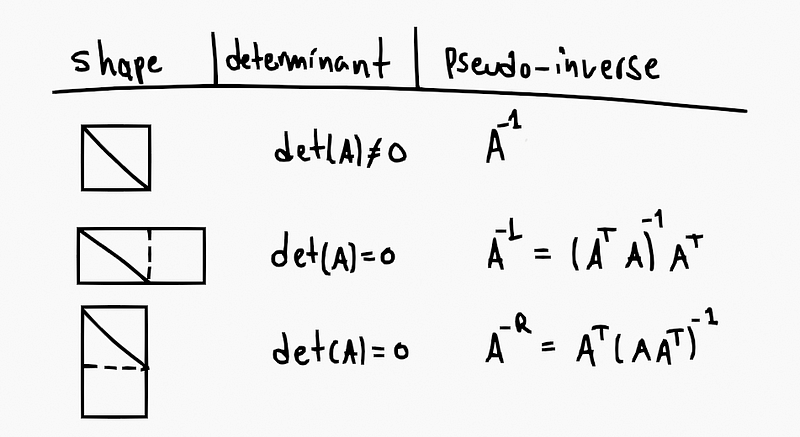
The shapes of a matrix and its respective pseudo-inverse and determinant

They are pretty similar to solving the inverse of a matrix, just adding a step, and multiplying by the transpose of the matrix before the calculation. But this could be from the left or the right. Which side it should be on depends on the dimensionality that encodes the core information.

A matrix encodes a transformation, a mapping from one space to another, and the dimensionality that we care about (the rank) is the smaller between the rows vs columns.

So if we have a matrix e.g. 3x5 (which would have det(A)=0), which is 3 rows and 5 columns, we look for a new matrix 3x3 that has a determinant. I don't know if it is clear that building matrix 5x5 from 3x5 would leads always a singular matrix (det(A)=0), because the core information is in the smaller, the row being dimensionality 3. Note: be sure to delete redundant, not linear independent vectors inside the matrix before these conclusions.

Parametric solution over the null space

Finding all the answers in terms of the free parameters or degrees of freedom. As it is not commonly taught it could be hard to figure out by ourselves, but it is simple.

If a matrix 3x4 has a problem with having an inverse, just take away one column and work with the first 3 ones, so we work out with a 3x3 matrix.

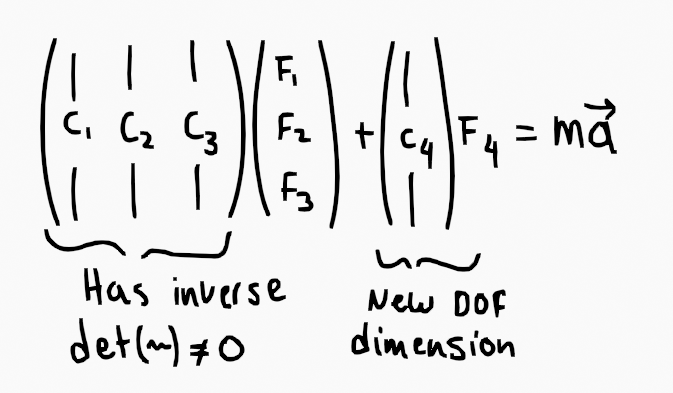
From 4x3 matrix to 3x3+1Dof

Since this is linear algebra, we can subtract from both sides C_4 * F_4, such that it is now placed on the right side. mmm, I like using A for notation matrices, so it may be a different one over examples. Here A is the matrix 3x3 that comes from the three first vectors. So:

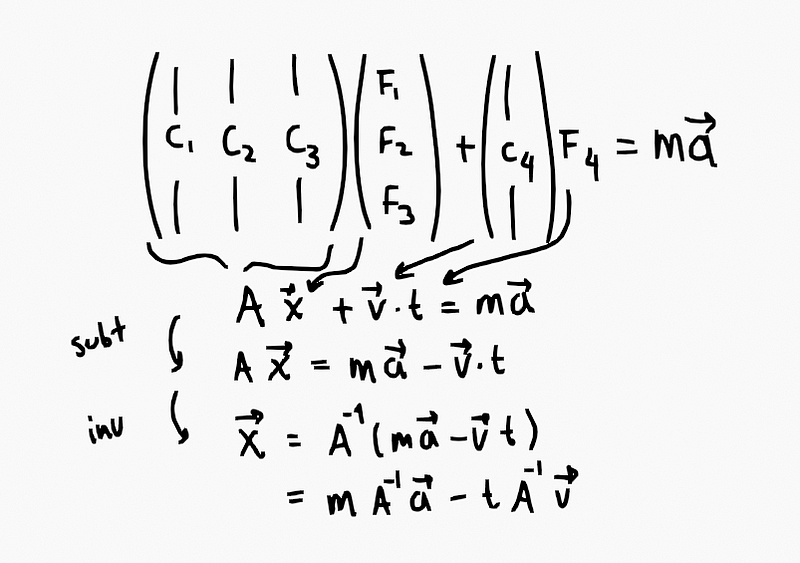
Doing algebra to isolate the desired variable x.

The fourth vector becomes the free parameter here, and in the image, F4 is renamed as 't'.

We renamed A, x, and t. Then applying algebra we subtract both sides trying to get 'x' alone, finally, we apply the inverse of A, as it now exists since det(A) is different from zero in a 3x3 linear independent vectors matrix.

Notice how the solution looks more closely:

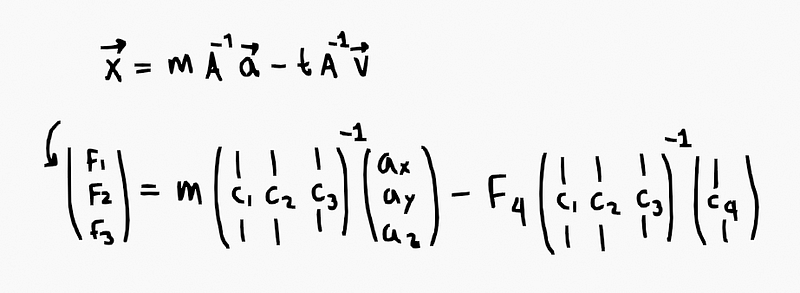
Expanding to keep track of the original variables.

but, even more abstractly now:

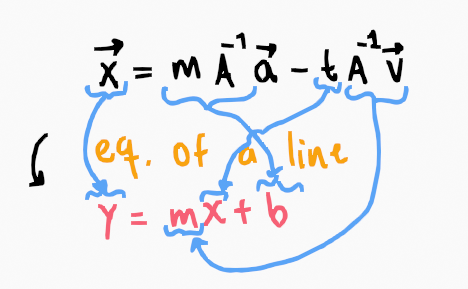
linking the parametric equation of a line and a linear system matrix equations

hehe, I couldn't avoid this meme 😅

Meme spoiler of this story

Connections: pseudo-inverse, parametric solution, and null space.

in short, without a lot of words, let's picture it:

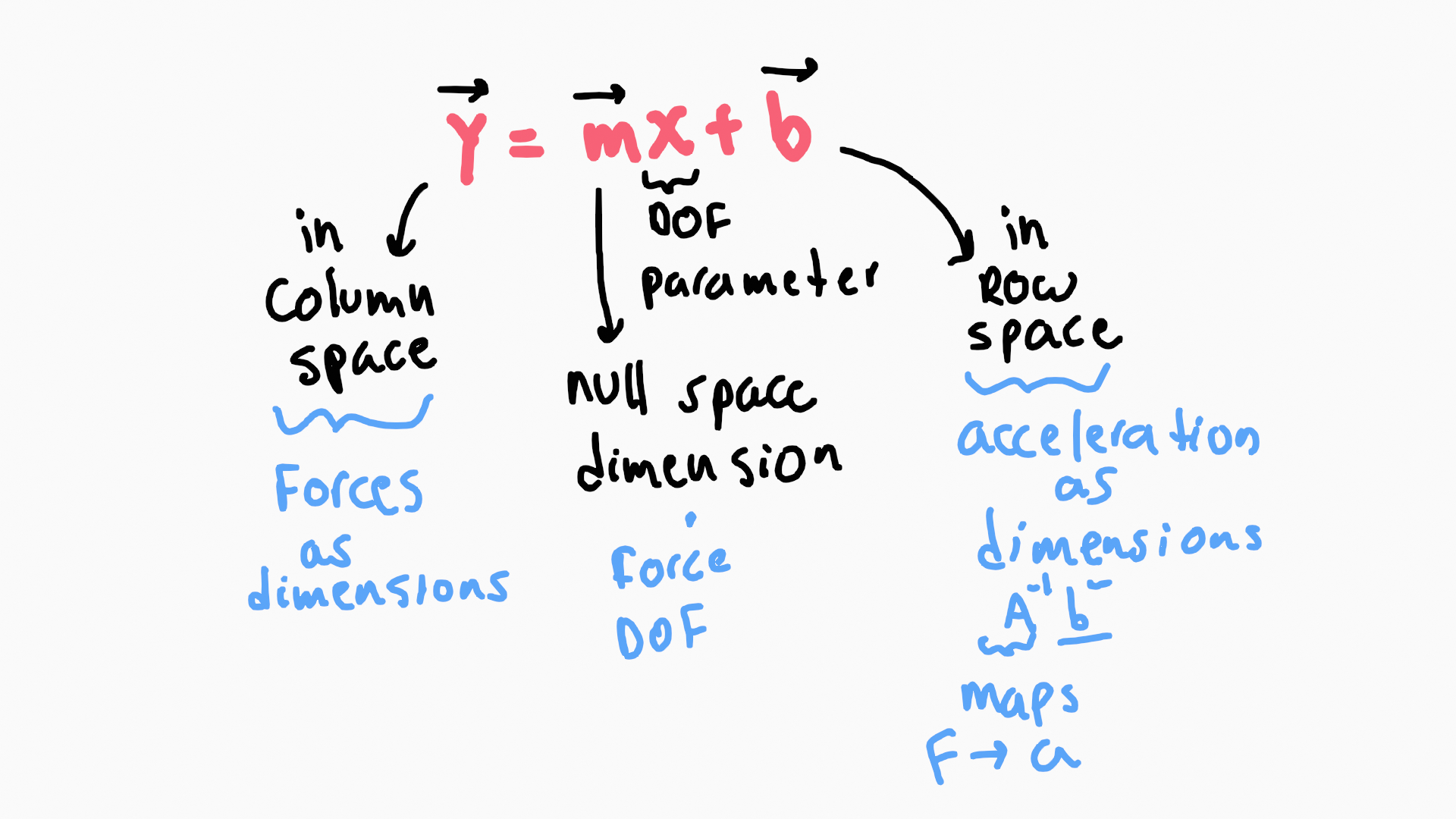
Getting intuition of the parametric equation form and the fundamental spaces.

and is missing the pseudo-inverse here… well, in short too, now that we have an intuition of it as a line equation, we could easily interpret the pseudo-inverse, or less square of forces minimization as:

Getting intuition of the optimal solution given by pseudo-inverse, and its relation with the null space

How this help to model a cable robot?

Now we can know which forces need to be pulled in the cables to get the desired acceleration, the acceleration leads at the same time to the velocity and the position if we include time variations.

The singular matrix, when the determinant is zero here, is not a problem anymore. We can find all the infinite solutions with the parametric form, and also the best one with the pseudo-inverse.

That's all for today friends! I hope you learned something new and cool, as I did. 🤓

I wished to do a numerical example here, maybe with Python code too, but this become large and it may deserve to be isolated in another story.

If you liked what I shared and want to stay tuned for future posts, feel free to follow me for the latest updates!

Thanks for reading this article!